巡检机器人关节电机的PID闭环控制系统的数学模型,针对复杂的作业环境以及机器人自身的一些因素会使模型参数产生一定摄动,常规PID控制效果差的问题,提出了基于Kharitonov理论的巡检机器人关节电机鲁棒PID控制方法,推导出了该控制系统鲁棒稳定的几个判定条件,给出了鲁棒PID参数稳定域的求取流程,最后基于Kharitonov理论对关节电机控制系统在Matlab中进行仿真实验。
结果表明,常规PID仅对标称系统控制效果好,对参数摄动系统控制效果欠佳,而鲁棒PID对参数摄动系统有较好的控制效果,且基于Kharitonov的鲁棒PID较基于H∞ 的鲁棒PID控制效果更优,满足了巡检机器人关节电机响应速度快、跟踪精度高、稳定性好的设计要求。
巡检机器人是一种沿高压架空输电线路行驶代替或者辅助人工巡检的特种电力作业机器人,在国民生产和日常生活中占有重要地位,应用前景非常广阔[1]。从控制的角度看,机器人的有效控制是保证正常巡检的前提,但是机器人存在多输入、多输出、强耦合、非线性等特征,使得在实际工程应用中从宏观上得到机器人完整精确模型很困难。
因此本文分解机器人的控制体系结构,从微观层面入手,以机器人的关节电机为研究对象,建立其PID闭环控制系统数学模型。考虑到关节电机PID参数很容易因野外恶劣气象条件、高空风载扰动、高电压强电磁干扰、以及电机的电枢反应,电机本身温度变化时,关节主电路的电阻,电感都会变化,这些都会影响电机标称值的改变。此外电机长时间的运行它与传动机构在结合处会的磨擦损耗,电机所带负载发生变化以及机器人运行在不同工况等,这些都会影响电机参数。
以上不确定性因素加大了机器人控制的难度,影响机器人机械臂控制的精度和稳定性。在某些极端情况下,可能引起机械臂与线路上绝缘子、悬垂线夹、防震锤等障碍物发生碰撞、干涉甚至从高压线上脱线,造成输电线和机器人的损坏和巨大经济损失。因此,在控制过程中必须根据系统的运行状态实时对机器人关节控制器的PID参数进行在线自适应调整,以确保在不确定性存在的情况下机器人在作业过程中依然保持较高的控制精度和较好的稳定性。
目前相关文献已提出了基于滑模变结构理论[2]、模糊理论[3]、神经网络[4]、遗传算法[5]及其相结合的很多的PID智能控制方法[6],但这些大都是在忽略不确定性因素和扰动的理想情况下进行的。HUANGYJ[7]、彭瑞[8]、徐峰[9]等人提出了基于区间多项式理论的参数不确定系统鲁棒控制方法,Ho M T[10]提出了基于H∞ 理论的鲁棒PID控制方法但被控对象大多数是针对工业控制系统而非机器人的关节电机。
吕永健[11]、恒庆海[12]等针对被控对象的抗干扰能力提出了直流电机的H∞ 鲁棒控制策略,但都只是单独的研究电机的鲁棒控制而没有联系到机器人。王鹏[13-14]等人在建立巡检机器人机械臂各类动作运动模型的基础上提出了基于HJI不等式的架空输电线巡检机器人的鲁棒控制,赵浩泉[15]等人提出了基于混合灵敏度的水下机器人鲁棒控制研究,刘开周[16]等人提出了基于结构奇异值的水下机器人鲁棒控制研究,
但这些都只是从宏观上对机器人的控制进行研究而没有具体到机器人各个关节的控制。因此,当前针对高压输电线路巡检机器人特别是从微观层面上分析关节电机鲁棒控制这方面的研究很少。1978年原苏联数学家卡里托诺夫提出了著名的Kharitonov定理,在处理参数不确定系统的鲁棒控制问题上取得了重大突破,基于此,本文将Kharitonov定理与关节电机的鲁棒控制结合起来,提出一种针对高压输电线巡检机器人关节电机参数不确定PID控制系统的鲁棒控制策略,其目的是控制机器人关节电机在存在不确定因素和扰动的情况下,稳定工作保持优秀的控制品质,为机器人正常巡检提供有力保障。
图1 巡检机器人控制体系结构
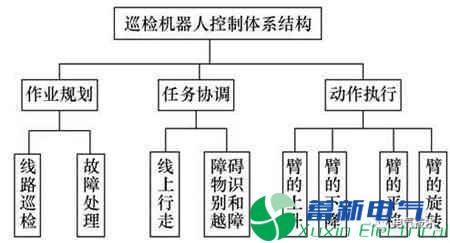
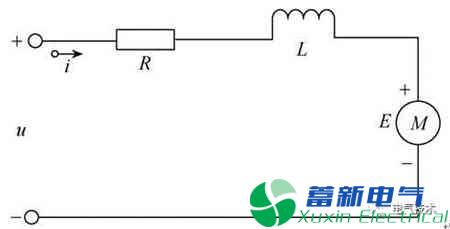
图2 巡检机器人关节电机电路模型
结论
本文在建立巡检机器人关节电机PID控制系统模型的基础上,利用Kharitonov定理对该模型进行了鲁棒稳定理论分析,利用Matlab仿真实验验证了本文理论分析的正确性。
值得进一步深入思考的是,本文被控对象分子为常数简化了计算量,在实际中可能会遇到理论上最多52个(充分条件4个+必要条件16个+充要条件32个)线性多项式的稳定性判断,计算量巨大,如何寻找简单易行的方法来处理这些多项式对提高算法的效率具有很大的实际意义。
此外,电机参数的摄动范围如何精确标定以及如何在保证机器人稳定运行的基础上,使各关节电机协调工作能耗更少,性能更优,将是后续研究的重要内容。






 手机扫描二维码
手机扫描二维码
