等效电源法指的是对于闭合电路中的定值电阻有时可以等效到电源的内部从而形成一个新的等效的电源。在此基础上对形成的新的电路进行分析使得问题简化,便于抓住主要问题并快速简捷地巧妙地解决问题。为掌握这种方法我们要理解相关知识:
电源最大输出功率的推导
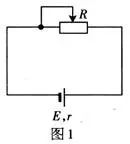
已知如图1所示的闭合电路中,电源的电动势为E,内阻为r,外电路电阻R为可变电阻,求当R为何值时电源有最大输出功率,输出功率为多少?
推导:电源的输出功率就是可变电阻消耗的功率。设电源的输出功率为P,则有:
.
由此式得,当外电路的电阻R等于电源的内阻r时其输出功率最大为。
有了上面的知识,我们利用等效电源法结合此结论可以对变值电阻的最大功率问题进行方便的解答,下面通过两个例题对此问题进行详细讲解。
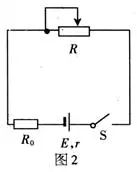
例1、如图2所示的电路中,电源的电动势为E=5V,内阻为r=10Ω,外电路中R0=90Ω,R为可变电阻,其阻值变化范围为0~400Ω,试求电阻R上消耗功率最大的条件和最大功率。
解析:采用等效电源法分析。我们把定值电阻R0等效到电源的内部,即把定值电阻与电源看做电动势为,内阻为的等效电源,R为外电路负载。如图3所示,则当R=R0+r=100Ω时,等效电源对外电路R0的输出功率最大。
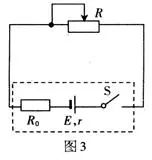
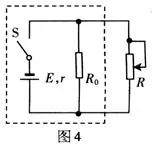
例2、如图4所示,电源电动势E=2V,内阻r=1Ω,电阻R0=2Ω,变值电阻的阻值范围为0~10Ω。求变值电阻为多大时,R上消耗的功率最大,最大值为多少?
解析:采用等效电源法分析。把定值电阻等效到电源的内部,即把电源和定值电阻看做电动势为,内阻为的电源,当时电源对外电路R的输出功率最大。
。
把数值代入各式得:
所以
总结:上面两题中两个定值电阻与电源分别为串联和并联的关系,所以等效电源的电动势和内阻表达式不同。当定值电阻与电源串联时等效电源的电动势等于电源电动势即E'=E,等效电源的内阻等于电源的内阻与定值电阻之和,即;当电源与定值电阻并联时,等效电源的电动势,等效电源的内阻等于电源的内阻与定值电阻的并联值,即。






 手机扫描二维码
手机扫描二维码
